DIFFUSION DE LA LUMIÈRE (météorologie)

DIFFUSION DE LA LUMIÈRE (météorologie)

On peut observer à l’ultramicroscope des particules de l’ordre du millième de micromètre en suspension dans un liquide ou dans un gaz, pourvu que ces particules soient suffisamment distantes les unes des autres. Lorsque leur concentration est trop élevée pour que le microscope puisse les séparer, leur ensemble diffracte un flux lumineux assez intense pour être perceptible à l’œil nu; on dit qu’il y a diffusion et l’ensemble des particules constitue un milieu trouble.

La diffusion joue un rôle particulièrement important en météorologie. Elle suit des lois qui dépendent de la dimension des particules par rapport à la longueur d’onde de la lumière qui les éclaire.

Cas des particules très petites par rapport à la longueur d’onde

Considérons un milieu trouble éclairé par un faisceau lumineux parallèle. Représentons par A cos 諸 t la vibration incidente de longueur d’onde en un point P; v est un élément de volume du milieu en ce point. D’après la théorie générale de la diffraction, cet élément se comporte comme une source en phase avec la vibration incidente, et on démontre qu’il envoie en un point M, à une distance MP = r, une vibration d’amplitude:

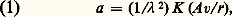où K représente un coefficient ne dépendant que des propriétés du milieu trouble.

L’intensité lumineuse correspondante s’écrit:

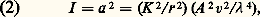d’où l’énoncé de la loi de Rayleigh: l’intensité diffusée par un milieu trouble est inversement proportionnelle à la quatrième puissance de la longueur d’onde de la lumière incidente.

Pour chaque radiation, le faisceau lumineux transmis par le milieu trouble transporte une énergie égale à la différence entre l’énergie incidente et l’énergie diffusée. Les radiations violettes, qui sont les plus affaiblies, sont moins bien transmises que les radiations rouges et, si la lumière incidente est blanche, la lumière transmise est d’autant plus fortement colorée en rouge que l’épaisseur traversée a été plus grande.

On explique la diffusion de la lumière par la vibration des électrons présents dans les molécules du milieu diffusant sous l’action du champ électrique transporté par l’onde lumineuse incidente, les déplacements de ces électrons produisant un champ électrique alternatif qui constitue la lumière diffusée.

Soit Oz la direction de propagation de l’onde incidente (fig. 1), que l’on suppose polarisée, Ox étant la direction du champ électrique correspondant; un électron placé en O effectue donc des vibrations parallèles à Ox.

Si on observe la lumière diffusée dans une direction OM faisant un angle avec Oz, la vibration M^x en M, parallèle à Ox, est perpendiculaire au plan yOz. Son amplitude a est indépendante de l’angle et ne dépend que de la distance OM.

Si la vibration incidente, et par suite la direction de la vibration de l’électron, est dirigée suivant Oy, la direction M^y de la vibration diffusée suivant OM est contenue dans le plan yOz et normale à OM; elle fait avec la direction d’oscillation Oy un angle égal à l’angle de OM avec Oz. L’amplitude de la vibration diffusée dans la direction OM est ainsi égale à a cos .

Si la lumière incidente est naturelle, on peut considérer qu’elle transporte deux vibrations dirigées l’une suivant Ox, l’autre suivant Oy avec des intensités égales; la lumière diffusée suivant OM contiendra les deux vibrations avec des intensités a ² et a ² cos² . Il y a donc prépondérance de la vibration M^x. La lumière diffusée par un milieu trouble dans une direction quelconque est ainsi partiellement polarisée; de plus, si la direction OM est normale à la direction Oz des rayons incidents (cos = 0), la composante M^y disparaît, la lumière diffusée étant totalement polarisée.

Diffusion moléculaire, bleu du ciel, absorption atmosphérique

Par temps clair, si on observe le ciel à 90⁰ du Soleil à travers un analyseur (lame Polaroid, par exemple), on constate que la lumière émise est fortement polarisée. D’autre part, la lumière provenant du ciel est bleue, et on peut penser que le bleu du ciel est dû à la diffusion de la lumière solaire par de très fines particules en suspension dans l’atmosphère. On admet que les particules diffusantes sont les molécules qui composent l’air.

Soit 猪 l’indice de réfraction de l’air, et n le nombre de molécules qu’il contient par centimètre cube. On démontre que, pour une molécule placée en O, l’amplitude diffusée en un point M de l’axe Oy à une distance OM = r a pour expression:

A représentant l’amplitude de la vibration incidente suivant Ox (fig. 1).

Pour une direction OM faisant un angle avec la direction des rayons incidents, l’intensité produite est a ² (1 + cos² ). Une intégration montre que le flux total 淋 diffusé dans tout l’espace par 1 centimètre cube d’air a pour expression: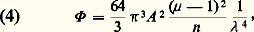

l’énergie lumineuse correspondante étant nécessairement empruntée au faisceau incident.

Considérons un faisceau parallèle de lumière naturelle transportant par centimètre carré un flux 淋 = 2 A ². La traversée d’une couche d’épaisseur dz entraîne la diffusion d’un flux d 淋 = 漣 淋 dz tel que:

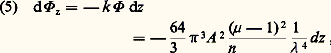en posant:

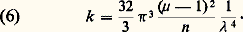Par intégration de la relation (5), on peut évaluer le flux 淋 transmis par une couche d’épaisseur z au moyen de la relation:

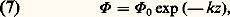淋 ⁰ désignant le flux incident.

Le coefficient k est dit coefficient d’absorption apparente, car l’absorption n’est pas réelle, les radiations incidentes n’étant pas transformées en chaleur, mais disséminées dans toutes les directions. Les relations (6) et (7) traduisent le fait que les radiations de courtes longueurs d’onde (radiations violettes), qui sont les plus diffusées, sont également les moins bien transmises.

L’absorption correspondante est d’ailleurs très faible. Pour l’air à la pression atmosphérique normale, 猪 漣 1 力 3.10^-4 et n 力 10¹⁹. Pour = 0,4 猪m, on trouve que k est très voisin de 4.10^-7 cm^-1. Supposons le Soleil au zénith et les rayons solaires traversant l’atmosphère normalement: l’énergie absorbée ne dépendant que du nombre de molécules rencontrées, l’absorption est la même que celle d’une colonne d’air de 1 centimètre carré de section ayant, à la pression normale, un poids égal à celui de 76 centimètres cubes de mercure. La longueur de cette colonne est L = 7,99.10⁵ cm et, dans ces conditions, le rapport 淋 / 淋 ⁰ de l’énergie solaire transmise à l’énergie incidente est obtenu en faisant z = L dans la relation (7). On trouve 淋 / 淋 ⁰ = 0,73. C’est bien l’ordre de grandeur que l’on obtient par des mesures directes.

Cas des particules de dimension supérieure à la longueur d’onde. Application aux nuages

Lorsque les dimensions des particules augmentent, les relations (1) et (2) ne sont plus valables et la relation (3) prend une forme compliquée, faisant intervenir à la fois l’angle , le rapport 見 = R / du rayon R des particules à la longueur d’onde de la lumière et leur indice de réfraction, mais cette forme se simplifie à nouveau pour des particules sphériques transparentes si le rapport 見 est supérieur à 5. Les particules se comportent alors comme de minuscules dioptres sphériques, auxquels on peut appliquer les lois de l’optique géométrique. C’est le cas des gouttelettes nuageuses dans le domaine visible (R 力 5 猪m).

Considérons une telle particule, de centre O, placée dans un faisceau parallèle d’axe Oz (fig. 2), et un rayon incident S I. Une partie de la lumière se réfléchit en I I , le reste se réfracte suivant I I¹. Une partie de l’énergie réfractée se réfléchit à l’intérieur, le reste se réfracte suivant I¹ I ¹; de même en I², I³, etc. En faisant la somme des différentes intensités lumineuses réfléchies ou transmises par la gouttelette dans une direction donnée, on obtient l’intensité totale diffusée dans cette direction. On trouve que cette intensité est presque entièrement concentrée au voisinage de la direction de propagation du faisceau. Le flux occulté par chaque gouttelette et emprunté au faisceau par ce processus est de la forme 淋 ¹ = E 神 R ², en représentant par E l’éclairement produit par le faisceau incident au niveau de la gouttelette.

Mais il faut également tenir compte de la diffraction par les bords de chaque gouttelette, dont le contour est assimilable à celui d’un écran circulaire opaque. La répartition des gouttelettes étant absolument irrégulière lorsqu’on observe le Soleil (constituant une source à l’infini) à travers un nuage peu épais, elles donnent une série d’anneaux de diffraction à l’infini. Le rayon angulaire 﨎 de ces anneaux est donné par la relation:

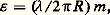où m prend les valeurs m ¹ = 5,14, m ² = 7,015, etc. Ils apparaissent violets à l’intérieur et rouges à l’extérieur; leur rayon angulaire est petit: pour 2R = 10 猪m et = 0,62 猪m, celui du premier anneau brillant est alors 﨎 = 5⁰ 45 .

D’après le théorème de Babinet, le flux 淋 ² diffracté par les bords d’un écran est égal au flux diffracté par le trou complémentaire. Il est donc égal au flux 淋 ¹ = E 神 R ² réfléchi et réfracté, de sorte que le flux total emprunté à l’onde incidente et diffusé par une gouttelette est égal à la somme 淋 ¹ + 淋 ², c’est-à-dire au double du flux intercepté par son contour, soit 淋 = E 2 神R ².

Si on a n gouttelettes, de rayon R , par centimètre cube de nuage, le coefficient d’absorption défini par la relation (7) a pour expression k = 2n 神R ². Les gouttelettes étant transparentes, il y a, dans ce cas aussi, absorption apparente. Pour n = 300 gouttelettes par centimètre cube, et R = 5 猪m, on trouve k = 4,7.10^-4 cm^-1. L’absorption apparente est ainsi environ 10³ fois plus grande que dans le cas de la diffusion moléculaire. Pour un nuage de 100 mètres d’épaisseur, le rapport 淋 / 淋 ⁰ correspondant à la relation (7) est de l’ordre de 1/100.

Le coefficient k ainsi défini est indépendant de la longueur d’onde: les radiations rouges et violettes subissent la même absorption apparente, et la lumière transmise par un nuage éclairé par le Soleil est blanche, ainsi que la lumière qu’il diffuse. Ce raisonnement n’est pas valable pour les radiations de grandes longueurs d’onde, car la condition R 礪 5 n’est plus vérifiée. Pour = 10 猪m, on trouve que le coefficient k est sensiblement réduit à la moitié de la valeur qu’il aurait dans le domaine visible. L’avantage que présente l’utilisation des sources infrarouges dans les problèmes de balisage est donc faible, compte tenu des difficultés qui en résultent d’autre part. Pour obtenir une amélioration sensible de la transparence, il faudrait utiliser des radiations de longueurs d’onde supérieures, mais celles-ci sont absorbées par la vapeur d’eau, ce qui les rend inutilisables pratiquement.

Il n’en est pas de même dans les atmosphères brumeuses; les dimensions des particules de brume, de l’ordre de quelques dixièmes de micromètre, sont nettement inférieures à la longueur d’onde des radiations infrarouges, dont l’emploi présente alors des avantages incontestables.

Encyclopédie Universelle. 2012.